Agathe Chollet

PhD
currently ATER in the LIM at the Reunion University


Introduction

CV

You can download my CV as a PDF file .

Qualifications

Thesis

I graduaded in december 2010 : the thesis as a PDF file.

It has been led at the Laboratoire Mathématiques Images et Application
MIA-MI (Math‑Images) team, La Rochelle university

My scientific advisors :

My thesis committee :

Research works

Keywords : Nonstandard Analysis, Discrete Geometry, Constructive Mathematics

Summary

We study the transition from the discrete to the continuous world in order to gain understanding of fundamental aspects of discrete geometry. Geometrical objects usually have a natural definition in the continuous world while it is difficult to find discrete analogous notions. Moreover, the computer treatment of these issues justifies the search of a constructive mathematical framework that offers an exact control of computations and an easy implementation.

From this double point of view, there exists an interesting numerical system because it is both discrete and continuous and it seems relatively constructive : this is the so-called Harthong-Reeb line which leads to the definition of the discrete analytical line by J.P. Reveillès.

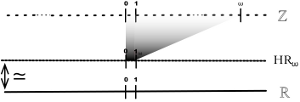Initially, we proposed a rigorous construction of the Harthong-Reeb line using a minimal form of nonstandard analysis. We described a process of arithmetization of continuous functions and we studied the constructive content of this system. Subsequently, we improved the constructive property of this numerical system by substituting the number theory of Laugwitz and Schmieden by usual nonstandard analysis. The new approach of the arithmetization process leads to the introduction of a discrete multi-resolution representation of continuous functions.

Our third step is to transfer these different notions in the Constructive Type Theory of Martin-Lof. The use of this framework, at the boundary between mathematics, logics and computer science, will guarantee a direct implementation in a high level computer language like Coq. An interesting consequence of our work on the Harthong-Reeb line is that this new numerical system appears as a new model of the constructive continuum.

Our programs are developed on a functional language OCaml. In parallel of the theoretical studies of the constructive content of our models, we prove with the formal proof management system Coq the validity of our proofs.

Ongoing Projects

Formalization and demonstration of our discrete/continuous reals models in Coq avec Nicolas Magaud

Publications

International conferences

International Journals

Teaching