Agathe Chollet

Docteur
Actuellement ATER au LIM à l'université de La Réunion


Introduction

CV

Vous pouvez télécharger mon CV au format PDF .

Qualifications

Thèse

J'ai soutenu ma thèse en décembre 2010 : le manuscrit au format PDF.

Elle a été réalisée au sein du Laboratoire Mathématiques Images et Application
Equipe MIA-MI (Math-Image), Université de La Rochelle

Mes encadrants scientifiques :

Mon jury de thèse :

Travaux de recherche

Mots-clefs : mathématiques nonstandard, mathématiques constructives, géométrie discrète, passage discret-continu

Résumé

Nous étudions le passage entre le discret et le continu dans le but d’obtenir une meilleure compréhension des aspects fondamentaux de la géométrie discrète. Les objets usuels de la géométrie ont des définitions naturelles dans le continu et il est difficile d’obtenir des notions analogues dans le discret.

D’autre part, le cadre des mathématiques constructives facilite le traitement sur machine de ces objets puisqu’il offre un contrôle exact sur les calculs et une implémentation plus aisée. Considérant ce double point de vue, il existe un système numérique intéressant du fait qu’il soit à la fois discret et continu et qu’il paraisse avoir des qualités constructives. Il s’agit de la droite d’Harthong-Reeb qui a notamment conduit à la définition de la droite discrète analytique par J.P. Reveillès.

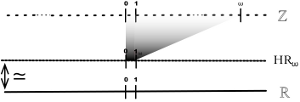Dans un premier temps, nous avons proposé une construction rigoureuse de la droite d’Harthong-Reeb en utilisant une forme minimale de l’analyse nonstandard. Nous avons décrit le processus d’arithmétisation de fonctions continues et avons étudié la part de constructivité de ce système.

Dans un second temps, nous avons amélioré les propriétés constructives de ce système numérique en substituant la théorie des nombres de Laugwitz et Schmieden à l’analyse nonstandard usuelle. Cette nouvelle approche a comme conséquences sur le processus d’arithmétisation d’introduire des aspects multi-échelle de représentation de fonctions continues.

Notre troisième étape est de transférer ces différentes notions dans la Théorie Constructive des Types de Per Martin-Lof. Ce cadre de travail, à la frontière entre mathématiques, logique et informatique, garantira une implémentation directe dans des hauts langages de programmation tel que Coq. Une conséquence intéressante de nos travaux sur la droite d’Harthong-Reeb est que ce nouveau système numérique apparait comme un nouveau modèle de continu constructif.

Nos programmes sont développés dans le langage fonctionnel OCaml. En parallèle des études théoriques du contenu constructif de nos modèles, nous assurons via l’assistant à la preuve Coq la validité de nos preuves.

Projets en cours :

Formalisation et démonstration de nos modèles de réels discrets/continus en Coq avec Nicolas Magaud

Publications

Conferences internationales

Revues internationales

Enseignement